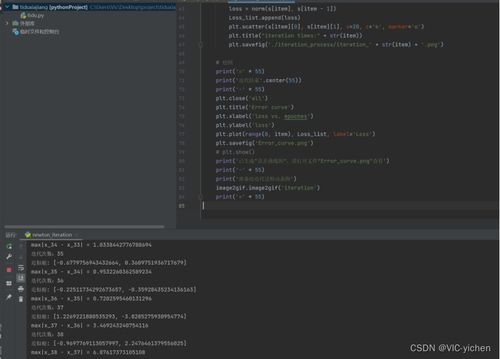
在人工智能领域,优化算法是支撑各类机器学习模型训练的核心技术。哈尔滨工业大学《人工智能数学基础》课程的实验三要求实现梯度下降法和牛顿法,这两种经典优化方法在人工智能基础软件开发中具有重要地位。
梯度下降法是最基础的一阶优化算法,其核心思想是沿着目标函数梯度的反方向迭代更新参数。在实验实现中,我们首先需要计算目标函数的梯度,然后设置合适的学习率进行迭代:x{k+1} = xk - η∇f(x_k)。该方法的优势在于实现简单、计算量小,特别适合大规模数据集。但同时也存在收敛速度慢、容易陷入局部最优等缺点。
相比之下,牛顿法是典型的二阶优化方法,不仅考虑梯度信息,还利用Hessian矩阵包含的曲率信息。其迭代公式为:x{k+1} = xk - [∇²f(xk)]^(-1)∇f(xk)。牛顿法具有二次收敛特性,在最优解附近收敛速度极快,但需要计算和存储Hessian矩阵,计算复杂度较高,且可能因Hessian矩阵不正定而导致算法失败。
在实验开发过程中,我们需要注意几个关键问题:首先是步长选择策略,对于梯度下降法可以采用固定步长、衰减步长或线性搜索;其次是收敛条件设置,包括梯度范数阈值、函数值变化量或最大迭代次数;最后是数值稳定性处理,特别是在牛顿法中需要对Hessian矩阵进行正则化处理。
通过对比实验可以发现,在条件良好的凸优化问题中,牛顿法通常表现出更快的收敛速度;而在高维非凸问题中,梯度下降法因其稳健性而更受青睐。现代深度学习框架如TensorFlow、PyTorch等都基于梯度下降的变种算法,同时也在特定场景下集成了牛顿法的改进版本。
这个实验不仅加深了我们对优化理论的理解,更为后续开发更复杂的人工智能系统奠定了坚实基础。掌握这些基础优化方法的工作原理和实现技巧,对于从事人工智能软件开发至关重要。